Soal dan Pembahasan - Ujian Tengah Semester Fungsi Kompleks B 2020 - Prodi Pendidikan Matematika FKIP ULM

Quote by Buzz Lightyear

To infinity and beyond

Soal Nomor 1
Jika $|z-1|=3$ buktikan bahwa $|z^2-2z-1|\leq 11$.

$\begin{aligned} |z^2-2z-1| &=|z^2-2z+1+(-2)| \\ &= |(z-1)(z-1)+(-2)| \\ &\leq |(z-1)(z-1)|+|-2| \\ &= |z-1||z-1|+|-2| \\ &= 3 \cdot 3 + 2 \\ &= 11 \end{aligned}$

Jadi, terbukti bahwa $\boxed{|z^2-2z-1|\leq 11}$.

Soal Nomor 2
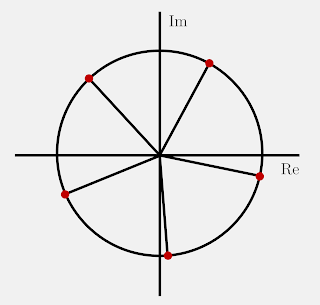
Tentukan semua akar dari $(2-2i\sqrt{3})^{\frac{1}{5}}$ kemudian gambarkan sketsanya.

Misal $z=(2-2i\sqrt{3})^{\frac{1}{5}}$
Ubah $z$ ke dalam bentuk polar.
$\begin{aligned} z&=(4~\text{cis}~(-\frac{\pi}{3}+2k\pi))^{\frac{1}{5}} \\ &=4^{\frac{1}{5}}~\text{cis}~(-\frac{\pi}{15}+\frac{2}{5}k\pi) \end{aligned}$
Didapat
$\displaystyle z_0=4^{\frac{1}{5}}~\text{cis}~(-\frac{\pi}{15})$
$\displaystyle z_1=4^{\frac{1}{5}}~\text{cis}~(-\frac{\pi}{15}+\frac{2}{5}\pi)=4^{\frac{1}{5}} \text{cis}~\frac{\pi}{3}$
$\displaystyle z_2=4^{\frac{1}{5}}~\text{cis}~(-\frac{\pi}{15}+\frac{4}{5}\pi)=4^{\frac{1}{5}} \text{cis}~\frac{11}{15}\pi$
$\displaystyle z_3=4^{\frac{1}{5}}~\text{cis}~(-\frac{\pi}{15}+\frac{6}{5}\pi)=4^{\frac{1}{5}} \text{cis}~\frac{17}{15}\pi$
$\displaystyle z_4=4^{\frac{1}{5}}~\text{cis}~(-\frac{\pi}{15}+\frac{8}{5}\pi)=4^{\frac{1}{5}} \text{cis}~\frac{23}{15}\pi$
Sketsa:

Soal Nomor 3
Tunjukkan bahwa fungsi $u(x,y)=y^3-3x^2y$ harmonik. Kemudian tentukan fungsi $v$ yang harmonik konjugat dengan $u$ dan nyatakan $u+iv$ dalam bentuk $f(z)$.

Fungsi $u(x,y)$ harmonik jika memenuhi persamaan Laplace, $\boxed{u_{xx}+u_{yy}=0}$

$u(x,y)=y^3-3x^2y$
$u_x = -6xy \hspace{75pt} u_y=3y^2 - 3x^2$
$u_{xx} = -6y \hspace{76pt} u_{yy}=6y $

Perhatikan bahwa $u_{xx}+u_{yy}=-6y+6y=0$, sehingga persamaan Laplace terpenuhi.
Jadi fungsi $u(x,y)$ harmonik.

Selanjutnya akan dicari fungsi $v$ yang harmonik konjugat dengan $u$.
Fungsi $v$ harmonik konjugat dengan $u$, maka haruslah fungsi $v$ memenuhi:
$\boxed{v_y=u_x}$ dan $\boxed{v_x=-u_y}$
Pertama, $v_y=u_x$, maka
$v_y=-6xy$
$v=\displaystyle \int -6xy~dy$
$v=-3xy^2 + g(x)$
dengan $g(x)$ adalah suatu fungsi terhadap $x$.
Berikutnya, $v_x=-u_y$.
$v_x=-(3y^2-3x^2)$
$\frac{\partial v}{\partial x} = -3y^2+3x^2$
$-3y^2 + g'(x)=-3y^2+3x^2$
$g'(x) = 3x^2$
$g(x) = x^3 + A$
dengan A suatu konstanta.
Sehingga diperoleh $\boxed{v=-3xy^2 + x^3 + A}$.

$\begin{aligned} f(x,y)&=u+iv \\ &=y^3-3x^2y + i(-3xy^2 + x^3 + A) \end{aligned}$ Untuk mengubah ke bentuk $f(z)$, dapat menggunakan metode Milne Thompson, yaitu dengan mensubstitusi $x=z$ dan $y=0$. Sehingga, \begin{aligned} f(z)&=0 + i(0+x^3+A) \\ &=i(x^3+A) \end{aligned} Jadi, $\boxed{v=x^3-3xy^2+A}$ dan $\boxed{f(z)=i(x^3+A)}$.

Soal Nomor 4
Tentukan semua nilai $z$ yang memenuhi $\cosh ⁡z=4i\sqrt{2}$.

$\begin{aligned} \cosh z &= \frac{e^z+e^{-z}}{2} \\ 4i\sqrt{2} &= \frac{e^z+e^{-z}}{2} \\ 8i\sqrt{2} &= e^z+e^{-z} \end{aligned}$
Kalikan kedua ruas dengan $e^z$, diperoleh
$e^z 8i\sqrt{2} = e^{2z} + 1$
Misalkan $x=e^z$
$8i\sqrt{2}x = x^2 + 1$
$x^2 - 8i\sqrt{2}x + 1 = 0$
Dengan rumus ABC, didapat akar-akar dari $x$
$\begin{aligned} x_{1,2}&=\frac{8i\sqrt{2} \pm \sqrt{-128-4}}{2} \\ &=4i\sqrt{2} \pm i\sqrt{33} \end{aligned}$
Didapat $x=e^z=4i\sqrt{2} \pm i\sqrt{33}$.

$e^z=4i\sqrt{2} \pm i\sqrt{33}$
$\ln e^z=\ln~(4i\sqrt{2} \pm i\sqrt{33})$
$z=\ln~((4\sqrt2 \pm \sqrt{33})i)$
Ingat bahwa $\ln z = \ln |z| + i\arg z$.
Karena $|4\sqrt2 \pm \sqrt{33})i|=(\sqrt{33} \pm 4\sqrt{2}$ dan $\arg = ((4\sqrt2 \pm \sqrt{33})i) = \pm \frac{\pi}{2} + 2k\pi$, maka
$z=\ln~(\sqrt{33} \pm 4\sqrt{2}) + i(\pm \frac{\pi}{2} + 2k\pi)$.

Perhatikan bahwa
$\ln~(\sqrt{33} - 4\sqrt{2})=\ln~\frac{(\sqrt{33}-4\sqrt{2})(\sqrt{33}+4\sqrt{2})}{\sqrt{33}+4\sqrt{2}} = \ln~\frac{1}{\sqrt{33}+4\sqrt{2}} = - \ln~(\sqrt{33}+4\sqrt{2})$

Jadi, didapat $\boxed{z=\pm \ln~(\sqrt{33}+4\sqrt{2}) + i(\pm \frac{\pi}{2} + 2k\pi)}$.

Catatan: Bentuk penting pada soal ini ada dua, yaitu
$\boxed{\cosh z = \frac{e^z+e^{-z}}{2}}$ dan $\boxed{\ln z = \ln |z| + i\arg z}$.